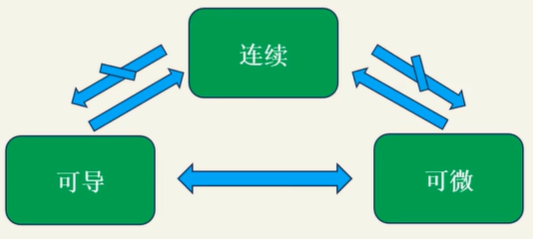
连续/可导/可微/可积

连续

对图像的直观理解：图像是连续不断的。

该点极限存在且和该点函数值相同。

定义

设函数 $f$ 在 $U(x_0)$ 邻域内有定义，若满足：

$$\underset{x\to x_0}{lim}f(x)=f(x_0)$$

则称 $f$ 在点 $x_0$ 连续。

增量形式定义

记：

• 自变量增量 $\mathrm{\Delta }x=x-x_0$
• 函数值增量 $\mathrm{\Delta }y=f(x_0+\mathrm{\Delta }x)-f(x_0)$

当 $\mathrm{\Delta }x\to 0$ 时，若满足：

$$\underset{\mathrm{\Delta }x\to 0}{lim}\mathrm{\Delta }y=0$$

则称 $f$ 在点 $x_0$ 连续。 （与极限定义等价）

连续性的三个判定条件

函数 $f$ 在 $x_0$ 处连续需同时满足：

1. $\underset{x\to x_0}{lim}f(x)$ 存在（$x_0$ 处有极限）
2. $f(x_0)$ 存在（$x_0$ 处有定义）
3. $\underset{x\to x_0}{lim}f(x)=f(x_0)$（极限值等于函数值）

增量形式定义

记：

• 自变量增量 $\mathrm{\Delta }x=x-x_0$
• 函数值增量 $\mathrm{\Delta }y=f(x_0+\mathrm{\Delta }x)-f(x_0)$

当 $\mathrm{\Delta }x\to 0$ 时，若满足：

$$\underset{\mathrm{\Delta }x\to 0}{lim}\mathrm{\Delta }y=0$$

则称 $f$ 在点 $x_0$ 连续。（与极限定义等价）

连续性的三个判定条件

函数 $f$ 在 $x_0$ 处连续需同时满足：

1. $\underset{x\to x_0}{lim}f(x)$ 存在（$x_0$ 处有极限）
2. $f(x_0)$ 存在（$x_0$ 处有定义）
3. $\underset{x\to x_0}{lim}f(x)=f(x_0)$（极限值等于函数值）

可导

对图像的理解：图像是光滑的。

不严谨：存在垂直切线（导数无穷）

定义

设函数 $y=f(x)$ 在点 $x_0$ 的某邻域 $U(x_0)$ 内有定义，若极限：

$$\underset{x\to x_0}{lim}\frac{f(x)-f(x_0)}{x-x_0}$$

存在，则称 $f$ 在点 $x_0$ 可导，该极限称为 $f$ 在 $x_0$ 处的导数，记作 $f^{\prime }(x_0)$。若极限不存在，则称 $f$ 在 $x_0$ 处不可导。

增量形式定义

记：

• 自变量增量 $\mathrm{\Delta }x=x-x_0$
• 函数值增量 $\mathrm{\Delta }y=f(x_0+\mathrm{\Delta }x)-f(x_0)$

导数可表示为：

$$f^{\prime }(x_0)=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x_0+\mathrm{\Delta }x)-f(x_0)}{\mathrm{\Delta }x}$$

导数的三种等价定义形式

① 标准形式：

$$\underset{x\to x_0}{lim}\frac{f(x)-f(x_0)}{x-x_0}$$

② 增量形式：

$$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x_0+\mathrm{\Delta }x)-f(x_0)}{\mathrm{\Delta }x}$$

③ 变量替换形式（令 $h=x-x_0$）：

$$\underset{h\to 0}{lim}\frac{f(x_0+h)-f(x_0)}{h}$$

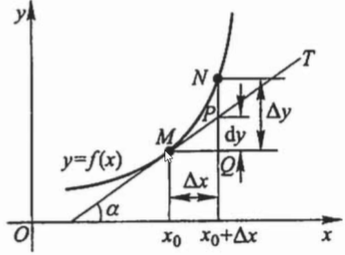
几何意义

导数 $f^{\prime }(x_0)$ 表示曲线 $y=f(x)$ 在点 $(x_0,f(x_0))$ 处切线的斜率：

• $\mathrm{\Delta }x$ 为自变量的变化量
• $\mathrm{\Delta }y$ 为函数值的变化量
• 当 $\mathrm{\Delta }x\to 0$ 时，$\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$ 的极限即为切线斜率

可导和连续的关系

结论1：可导一定连续，连续不一定可导

图像直观理解

可导：光滑

连续：连绵不断

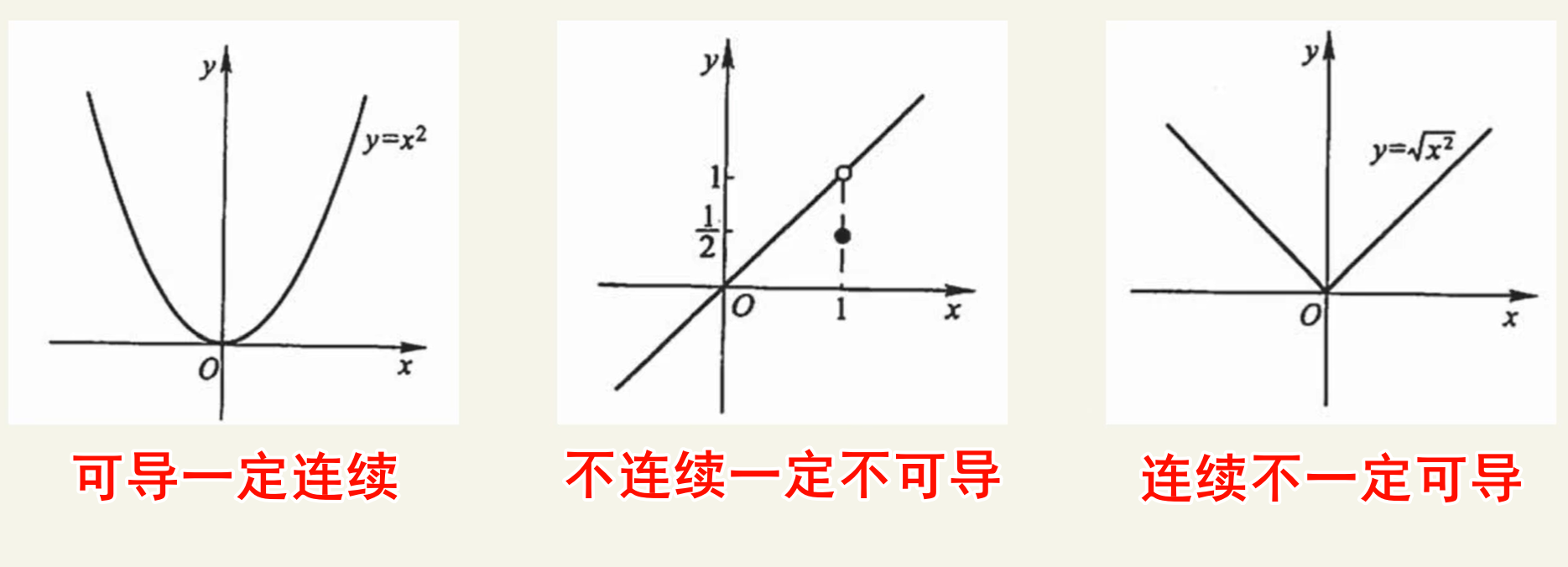
定义直观理解

函数连续定义：$$\lim_{\Delta x \to 0} \Delta y = 0$$

函数可导的定义：$$\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} \text{ 极限存在}$$

可导一定连续：假如$$\frac{\Delta y}{\Delta x}$$分子不为0，当分母趋近于0时，极限一定不存在，趋近于正无穷或者负无穷因此分母一定为0，即函数连续。

连续不一定可导：$$\Delta{y}$$为0，$$\frac{\Delta y}{\Delta x}$$零比零型极限不一定存在

严格证明

可导 ⇒ 连续

设 $f(x)$ 在 $x_0$ 处可导，即存在 $f^{\prime }(x_0)$ 满足：

$$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=f^{\prime }(x_0)$$

其中 $\mathrm{\Delta }y=f(x_0+\mathrm{\Delta }x)-f(x_0)$

构造无穷小量：

$$\epsilon =\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}-f^{\prime }(x_0)(\mathrm{\Delta }x\to 0\text{时}\epsilon \to 0)$$

两边同时乘$$\Delta x$$变形得函数增量表达式：

$$\mathrm{\Delta }y=f^{\prime }(x_0)\mathrm{\Delta }x+\epsilon \mathrm{\Delta }x$$

当 $\mathrm{\Delta }x\to 0$ 时：

$$\underset{\mathrm{\Delta }x\to 0}{lim}\mathrm{\Delta }y=0⟹\underset{x\to x_0}{lim}f(x)=f(x_0)$$

故 $f$ 在 $x_0$ 处连续。

反例说明（连续 ⇏ 可导）

以 $y=\sqrt[3]{x}$ 在 $x=0$ 处为例：

1. 连续性验证：

   $$\underset{x\to 0}{lim}\sqrt[3]{x}=0=f(0)$$

   满足连续定义。

2. 不可导性验证：

   $$f^{\prime }(0)=\underset{h\to 0}{lim}\frac{\sqrt[3]{h}-0}{h}=\underset{h\to 0}{lim}\frac{1}{h^{2/3}}=+\mathrm{\infty }$$

   导数趋向无穷，故不可导。

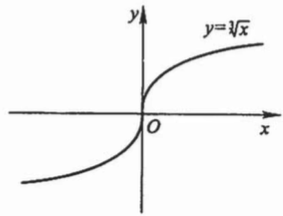
以下情形会导致连续但不可导：

• 存在垂直切线（导数无穷）
• 存在尖点（左右导数不相等）
• 振荡间断（如 $y=x\sin (1/x)$ 在 $x=0$ 处）

可微

概念引入

设一边长为 $x_0$ 的正方形，它的面积 $S=x_0^2$。
若边长增量为 $\mathrm{\Delta }x$，则面积增量：

$$\mathrm{\Delta }S=(x_0+\mathrm{\Delta }x{)}^2-x_0^2=2x_0\mathrm{\Delta }x+(\mathrm{\Delta }x{)}^2$$

直观理解：
当 $x_0$ 有微小增量 $\mathrm{\Delta }x$ 时，面积增量 $\mathrm{\Delta }S$ 可近似用第一部分 $2x_0\mathrm{\Delta }x$ 代替，误差为 $(\mathrm{\Delta }x{)}^2$（关于 $\mathrm{\Delta }x$ 的高阶无穷小量）。

定义

设函数 $y=f(x)$ 在点 $x_0$ 的某邻域 $U(x_0)$ 内有定义。当 $x_0$ 有增量 $\mathrm{\Delta }x$（$x_0+\mathrm{\Delta }x\in U(x_0)$）时，函数增量为：

$$\mathrm{\Delta }y=f(x_0+\mathrm{\Delta }x)-f(x_0)$$

可微的判定：
若存在常数 $A$，使得 $\mathrm{\Delta }y$ 可表示为：

$$\mathrm{\Delta }y=A\mathrm{\Delta }x+o(\mathrm{\Delta }x)$$

则称 $f$ 在点 $x_0$ 可微，并称 $A\mathrm{\Delta }x$ 为 $f$ 在 $x_0$ 的微分，记作 $dy$，即：

$$dy=A\mathrm{\Delta }x$$

关键性质：

• 微分 $dy$ 与增量 $\mathrm{\Delta }y$ 仅相差一个高阶无穷小量。
• 当 $A\ne 0$ 时，$dy$ 是 $\mathrm{\Delta }y$ 的线性主部（$\mathrm{\Delta }x$ 的线性函数）。

可微和可导的关系

结论2： 函数 $ f $ 在点 $x_{0} $ 处可微的充要条件是 $ f $ 在 $ x_{0} $ 处可导，且微分系数 $ A = f'(x_{0}) $。

证明

必要性（可微 ⇒ 可导）

若 $ f $ 在 $ x_{0} $ 可微，由定义：

$$\mathrm{\Delta }y=A\mathrm{\Delta }x+o(\mathrm{\Delta }x)$$

两边除以 $ \Delta x $：

$$\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=A+\frac{o(\mathrm{\Delta }x)}{\mathrm{\Delta }x}$$

取极限 $ \Delta x \to 0 $：

$$f^{\prime }(x_0)=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=A$$

即 $ f $ 在 $ x_{0} $ 可导，且 $ A = f'(x_{0}) $。

充分性（可导 ⇒ 可微）

若 $ f $ 在 $ x_{0} $ 可导，即极限存在：

$$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=f^{\prime }(x_0)$$

由极限定义，可设：

$$\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=f^{\prime }(x_0)+\epsilon (\epsilon \to 0\text{ 当 }\mathrm{\Delta }x\to 0)$$

整理得：

$$\mathrm{\Delta }y=f^{\prime }(x_0)\mathrm{\Delta }x+\epsilon \mathrm{\Delta }x$$

其中 $ \varepsilon \Delta x = o(\Delta x) $，故满足可微定义：

$$\mathrm{\Delta }y=f^{\prime }(x_0)\mathrm{\Delta }x+o(\mathrm{\Delta }x)$$

因此 $ f $ 在 $ x_{0} $ 可微，且 $ dy = f'(x_{0})\Delta x $。

总结

1. 可微 ⇔ 可导：函数在某点可微与可导等价，且微分系数 $ A $ 即为导数 $ f'(x_{0}) $。
2. 微分表达式：$$dy=f^{\prime }(x_0)\mathrm{\Delta }x$$或写作 $ dy = f'(x_{0})dx $（当 $ \Delta x $ 记为 $ dx $ 时）。
3. 几何意义：==微分 $ dy $ （近似值）是函数增量 $ \Delta y $（准确值） 的线性主部，用切线近似代替函数变化==。

连续、可导、可微之间的关系

可积

定义

分割（定义1）

设闭区间 $[a,b]$ 上有 $n-1$ 个点，依次为：

$$a=x_0<x_1<x_2<\cdots <x_{n-1}<x_n=b$$

这些点将 $[a,b]$ 划分为 $n$ 个小区间 ${\mathrm{\Delta }}_i=[x_{i-1},x_i]$（$i=1,2,\dots ,n$）。

• 分割表示：记为 $T=\{x_0,x_1,\dots ,x_n\}$ 或 ${\mathrm{\Delta }}_1,{\mathrm{\Delta }}_2,\dots ,{\mathrm{\Delta }}_n$。
• 小区间长度：$\mathrm{\Delta }{x}_i=x_i-x_{i-1}$。
• 分割模：$\parallel T\parallel =\underset{1\le i\le n}{max}\{\mathrm{\Delta }{x}_i\}$，表示最大子区间长度。

---

积分和（定义2）

设 $f(x)$ 是定义在 $[a,b]$ 上的函数，对于分割 $T=\{{\mathrm{\Delta }}_1,{\mathrm{\Delta }}_2,\dots ,{\mathrm{\Delta }}_n\}$，任取点 ${\xi }_i\in {\mathrm{\Delta }}_i$（$i=1,2,\dots ,n$），作和式：

$$\sum _{i=1}^{n}f({\xi }_i)\mathrm{\Delta }{x}_i$$

称为 $f(x)$ 在 $[a,b]$ 上的积分和（黎曼和）。

---

可积性（定义3）

设 $f(x)$ 定义在 $[a,b]$ 上，$J$ 为确定的实数。若对任意 $\epsilon >0$，存在 $\delta >0$，使得对 $[a,b]$ 的任意分割 $T$ 及任意选取的点集 $\{{\xi }_i\}$，只要 $\parallel T\parallel <\delta$，就有：

$$|\sum _{i=1}^{n}f({\xi }_i)\mathrm{\Delta }{x}_i-J|<\epsilon$$

则称 $f(x)$ 在 $[a,b]$ 上可积（黎曼可积），$J$ 称为 $f(x)$ 在 $[a,b]$ 上的定积分（黎曼积分），记作：

$$J={\int }_a^{b}f(x)dx$$

极限表示

定积分也可用极限符号表示：

$$J=\underset{\parallel T\parallel \to 0}{lim}\sum _{i=1}^{n}f({\xi }_i)\mathrm{\Delta }{x}_i={\int }_a^{b}f(x)dx$$

关于可积的几个重要结论

1. 可积的充分条件

① 连续函数可积：
设 $ f $ 为 $[a,b]$ 上的连续函数，则 $ f $ 在 $[a,b]$ 上必可积。
（连续函数在闭区间内一致连续，保证振幅可控）

② 有限间断点的有界函数可积：
若 $ f $ 在 $[a,b]$ 上有界，且只有有限个第一类间断点（跳跃间断点），则 $ f $ 在 $[a,b]$ 上可积。
（间断点贡献的积分和误差可被限制）

2. 可积的必要条件

有界性要求：
若函数 $ f $ 在 $[a,b]$ 上可积，则 $ f $ 在 $[a,b]$ 上必定有界。
（无界函数的积分和会发散，无法收敛到有限值）

---

3. 可积的充要条件（可积准则）

定理表述：
函数 $ f $ 在 $[a,b]$ 上可积的充要条件是：
对任意 $ \varepsilon > 0 $，存在分割 $ T $，使得上和 $ S(T) $ 与下和 $ s(T) $ 满足：

$$S(T)-s(T)<\epsilon$$

关键概念：

• 上和 $ S(T) $：取每个子区间上 $ f(x) $ 的上确界 $ M_i $，求和 $ \sum M_i \Delta x_i $。
• 下和 $ s(T) $：取每个子区间上 $ f(x) $ 的下确界 $ m_i $，求和 $ \sum m_i \Delta x_i $。

多元函数

多元函数：可微一定可导，可微一定连续，偏导连续一定可微，偏导存在不一定连续。

可偏导不能推出连续：偏导只能管住当前偏导方向的数（该点极限趋近于某个数），其他方向管不到

同理，可偏导推不出可微：可微是全增量，跟一领域内的点上函数值都是有关系的，但是偏导只能（例如二元函数，偏导只跟两个方向上那两条线有关，决定不了其他临近点的变化趋势）。一元函数可以是因为X方向导数可以决定领域内所有函数

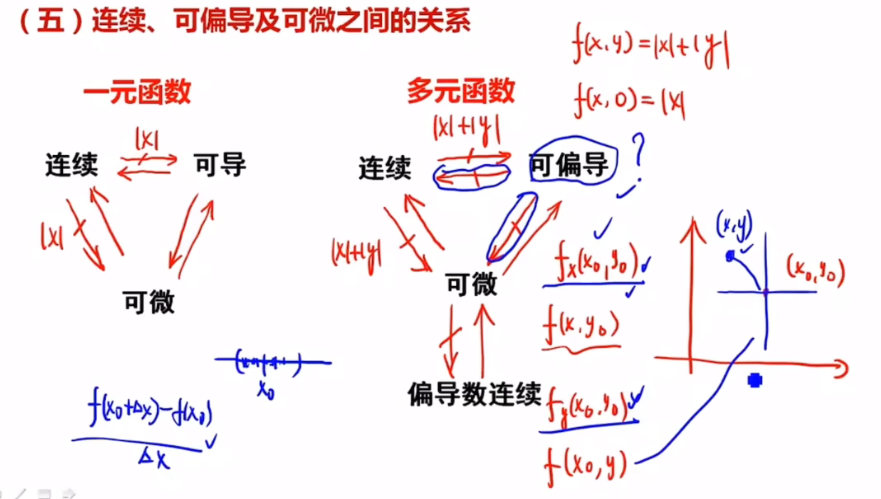
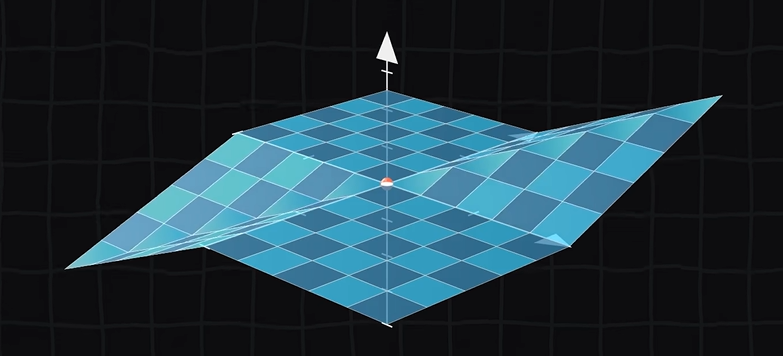
函数可微性：在某点附近局部很平（无论怎么放大放大再放大都不“尖”），光滑===>附近的坡度多大方向导数就多大，光滑说明所有方向上导数存在，但是多元偏导只能保证多个方向上（几元几个方向）的光滑。

例如下图原点，x、y、z三个方向均可导，有方向导数：

Reference

连续/可导/可微/可积，一个视频理解清楚bilibili

[6分钟速通可微和可导直观理解]_哔哩哔哩_bilibili