Batch Normalization vs Layer Normalization

Batch Normalization

李宏毅
李沐

Feature Scaling

Make different features have the same scaling

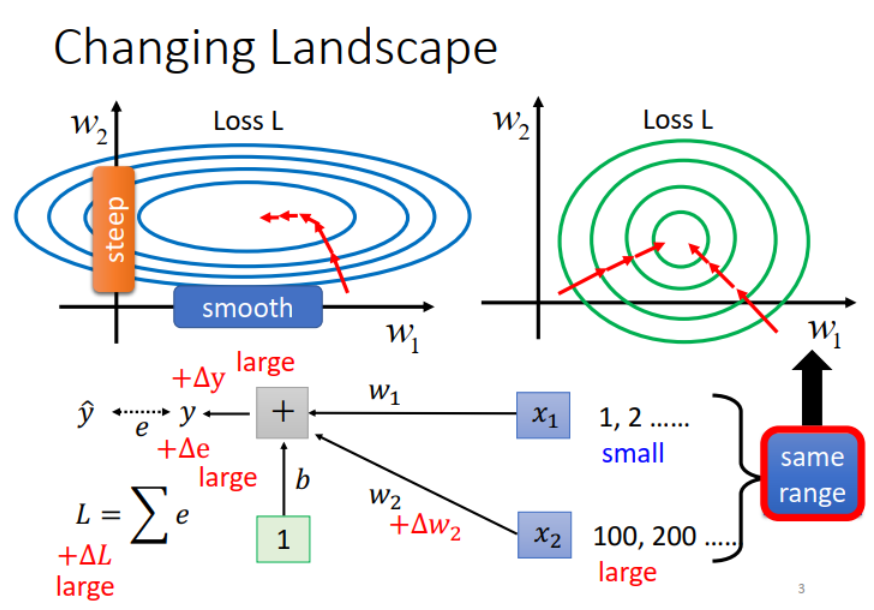
假设 x1 的 scale 非常小、x2 的 scale 非常大。当 x1 和 x2 变动时，由于 x2 的 scale 比较大，而 x2 要和 W2 相乘，因此 W2 的变动相对于 W1 会对 Loss 产生更多影响（gradient在横的方向上和纵的方向上变化很不一样，让train变得很不容易，因为不同方向上需要不同的learning rate），也因此会产生下面这种图。

如果对不同的feature做normalization（右图）使得error surface 变成正圆，可以让training变得容易很多

Feature Normalization
假设 $x^1$, $x^2$, ...,$x^R$表示一组输入 samples，把它们在每个维度 (feature) 上减去相应的均值 (mean)，除以对应的方差 (variance)，如下图中公式所示。做完 normalization 之后，输入 samples 每个维度上的均值都是 0，方差是 1。

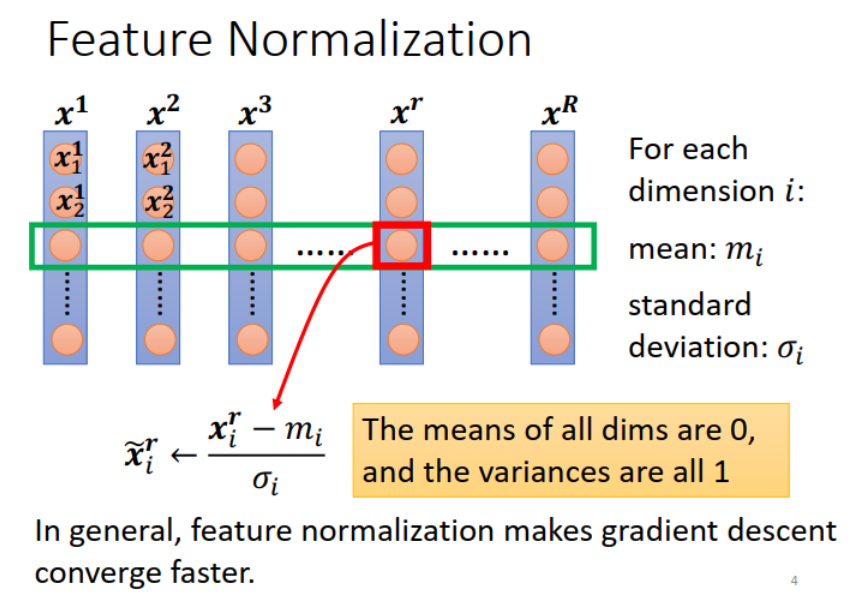
做了feature normalization之后往往会让training变得更加快速

思考：对于deep learning中的每一层是不是都可以做feature normalization 让结果learn的更好

可以，解决内部协变量偏移(Internal Covariate Shift)问题。

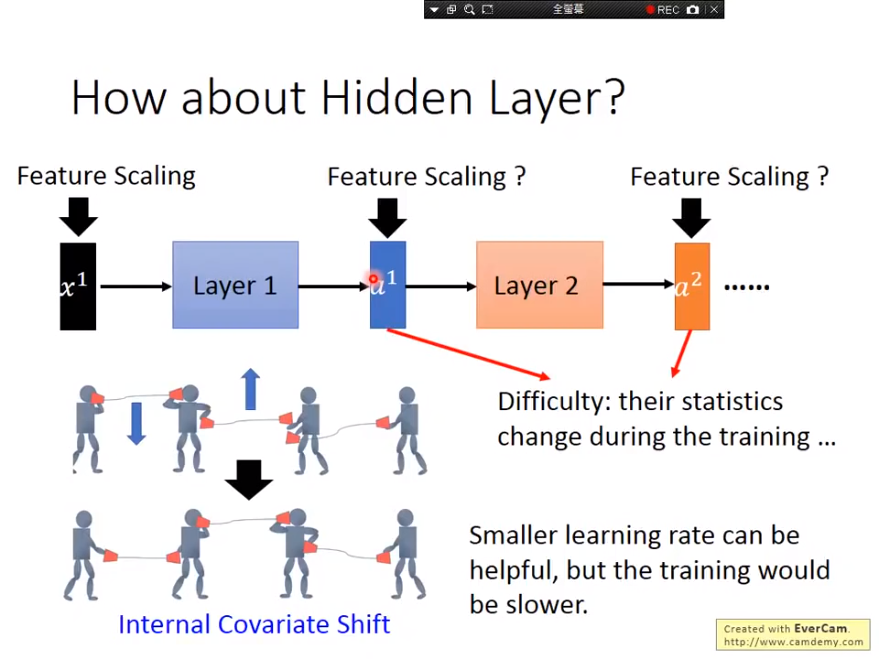
内部协变量偏移: 下图为例，有四个人，每个人代表一个Layer，中间利用话筒来做讯息的传递，线直了代表沟通顺畅，观察左二的人，左手话筒高，右手话筒低，这时候左一的人跟他说，左手话筒低一点，右二的人跟他说，右手话筒高一点，然后左二照做就可以变下图那样，左手过低，右手过高。 两个都变化，结果反而坏掉了。

传统方法，learning rate小一点，但是会慢很多

当网络很深的时候，反向传播传到前面时gradient往往会逐渐变小，这导致后面层很快就收敛了，但是前面的层变化很小，收敛很慢。同时一旦前面的层发生改变，后面的层又需要跟着重新train。
前面训练慢，后面训练快，但前面一改变，后面需要重新跟着训练。

能否在底部训练的时候避免变化顶部?

如果可以对每一层都Featuer Scaling，让它们的均值、方差皆缩放至一个值域内，那对下一个Layer而言，它的Statistics就是固定而不会上下飘动，训练上可能就可以更加的容易。
保证层间输出和梯度符合某一特定分布，以提高数据和损失的稳定性。 Feature Normalization对输入数据很有用，因为输入数据不会改变，但是对隐藏层就不管用了。每一个Layer的Output都是一直变化的，因为模型参数是不断变化。

所以发明了Batch Normalization解决这个问题。

Batch Normalization

Batch（批）

Batch意指在训练过程中每次取一把出来计算，下图范例一次取三笔数据出来平行运算，但在GPU计算中会将三个Vector转成Matrix，以此加速计算速度。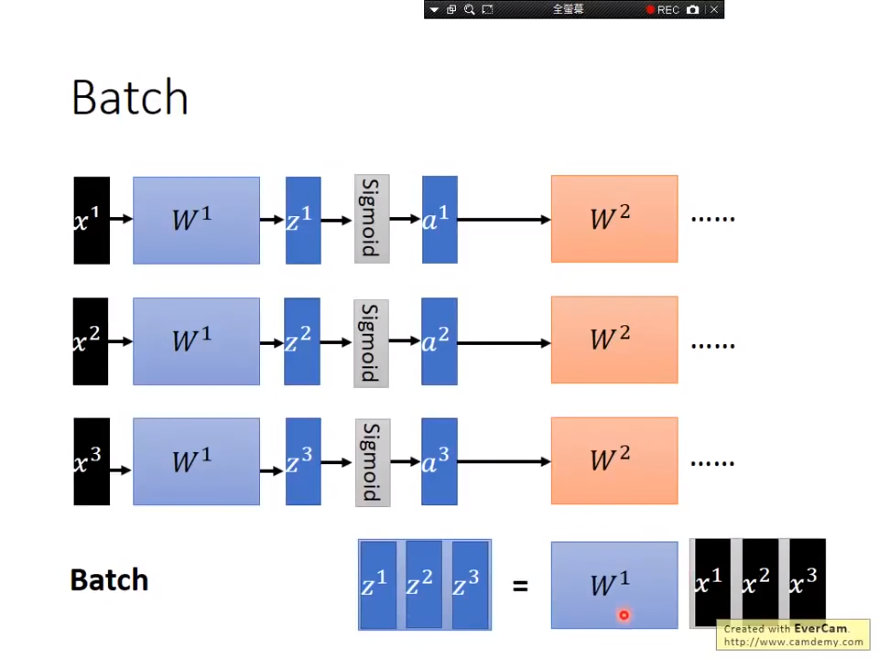

BN

Batch normalization可以实作在activation function的input或output，但论文较多是作在input，也就是在计算出z之后就先经过BN再执行activation function，这么做的好处在于可以确保不会让值域落在微分值较小的地方， 以为Sigmoid例，如果值域落在两端极值，那微分值太小，不好收敛。

注意到一点，在实作BN的时候我们希望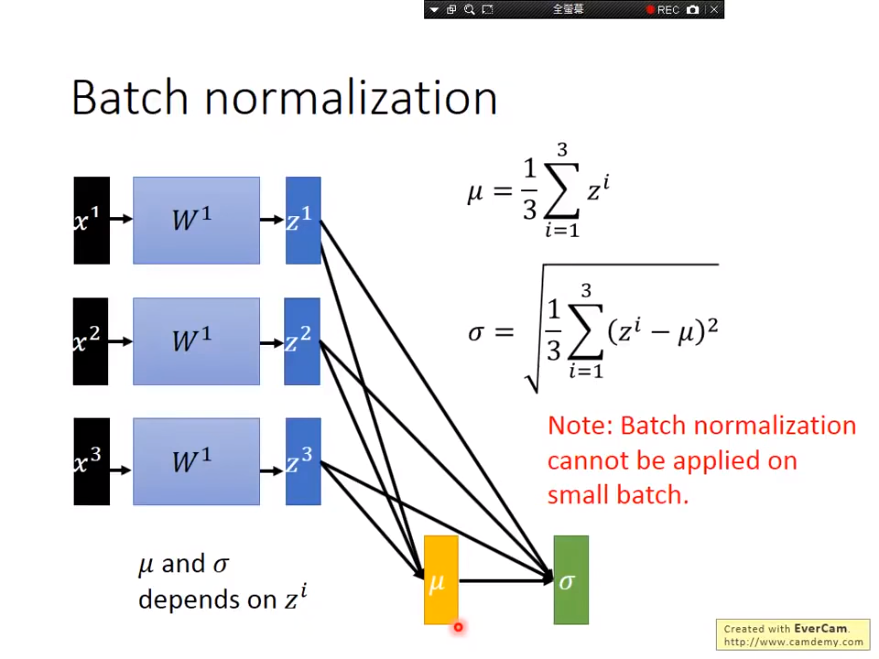$\mu$ $\sigma$所代表的是全体资料集的随机性，但是计算整个资料集的随机性是非常耗费时间的一件事，而且权重的数值会不断改变，不可能每一次迭代之后就重新再计算整个资料集，因此在实作BN的时候我们只会以计算该Batch， 这代表所使用的Batch Size必须要够大，这样子才有办法从Batch去估测整个资料集。batch size 很小，比如说等于 1 时，求不了均值和方差，没有意义。

把输入 samples 的各个维度都调整成均值为 0，方差为 1的分布，有时可能不好解决问题，此时可以做一点改变（学到一个新的均值β，新的方差γ）。如下图右上角的公式所示。注意： γ 和 β 的值通过学习得到，也就是根据模型和数据的情况调整。 γ 初始设为全 1 向量， β 初始设为全 0 向量。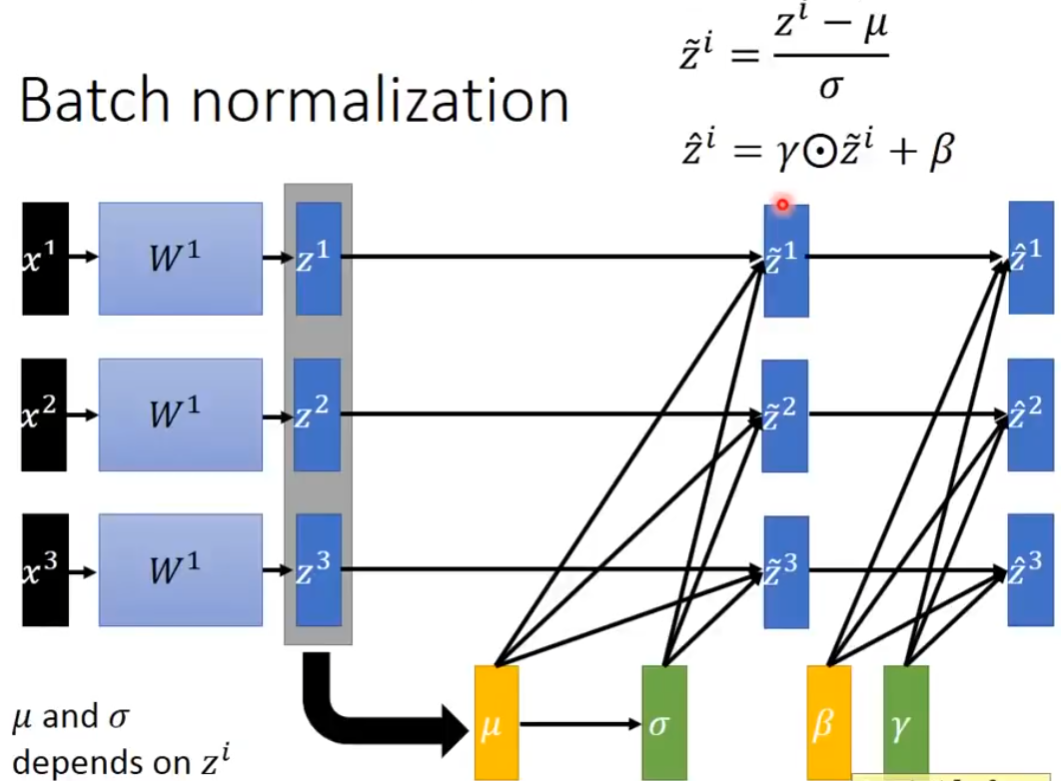

m个样本，每个样本n个特征，就是一个m*n的矩阵，BN就是对每一列（共n个列）分别求均值和方差
每个像素点（通道数为100）作为一个样本，相当于它是一个具有100维特征的样本

如何测试

但在测试过程中的一个问题在于，训练过程可能是Batch，但测试的时候却可能是一笔资料，只有一笔资料是估不出$\mu$ $\sigma$，怎么办？

• 一种作法是在训练结束之后，参数已经确定不再变动更新，这时候估算整个资料集的$\mu$ $\sigma$，但如果资料集过大或是online training，数据根本没有留存的情况下是无法这么执行的。
• 另一种作法是将过程中的$\mu$ $\sigma$计算平均，但训练过程中的参数不断变化，得到的$\mu$ $\sigma$也差异过大，因此较能执行的作法是让训练结束前的区间有较大的权重，初始训练过程中的区间给予较小的权重， 如RMSProp

代码实现

import torch
from torch import nn
from d2l import torch as d2l

# 对哪一个纬度求均值，对应的那个纬度就会变成1，dim=0 表示求完均值之后会生成一个（1*列数）的向量，所以也就是给每一列求均值
# mean = X.mean(dim=0)
# dim＝(0,2,3)，输出1*n*1*1的特征矩阵，通道的维度是保留着的
# dim等于哪一维，就相当于把那一维揉成一坨

def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    """
    X: 这一层的输入
    gamma, beta: 可以学习到的参数
    moving_mean, moving_var: 全局的均值和方差，在做推理的时候用到
    eps: 为了避免除0
    momentum: 更新moving_mean, moving_var，一般取0.8，0.9
    """
    
    # 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
            # 这里我们需要保持X的形状以便后面可以做广播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data

class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

优点

• 解決Internal Covariate Shift的問題，从此不再只能设非常小的值lr
• 有效解決geadient 消失/爆炸，确保Output都在0的附近（斜率较大的地方）
• 模型受权重初始化的影响较小，当权重乘上k倍，$\mu$ $\sigma$也都有k倍的影响，分子分母皆有k倍影响就代表什么没有影响。
• 有人说，BN可以减少overfitting的问题（如果数据有偏移，可以把他normalization回来），有正规化的效果。

对随机的小偏量内部添加噪音，确保学习的健壮性

总结

• 一般用在较深的网络中
• 批量归一化固定小批量中的均值和方差，然 后学习出适合的偏移和缩放
• 可以加速收敛速度（学习率可以调大），但一般不改变模型精度

Layer Normalization

LayerNorm（Layer Normalization）是2016年提出的，随着Transformer等模型的大规模推广，LayerNorm出现频率也随之越来越高。其大体思想类似于BatchNorm，对输入的每个样本进行归一化处理，具体就是计算每个输入的均值和方差，归一化到均值为0，方差为1，另外还会学习$g$和$b$来将方差和均值缩放从任意值。

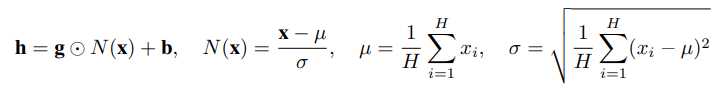
LayerNorm可以帮助模型收敛，原文中解释是因为其对输入进行了归一化操作，使得数据的分布更加稳定。

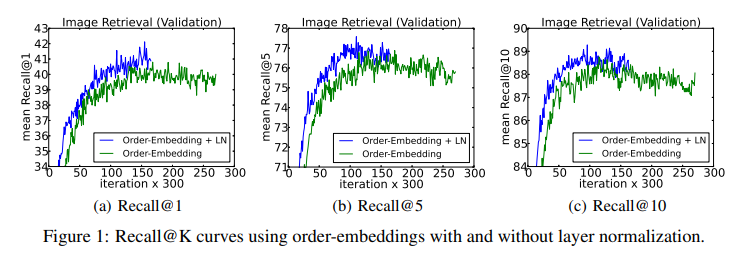
另外一篇文章Understanding and Improving Layer Normalization从梯度的角度对LayerNorm进行了分析，这篇文章的作者发现了以下两个结论，并提出了一个改进方法称为AdaNorm。

• LayerNorm 中引入的 gain 和 bias，可能会导致 overfitting，去掉他们能够在很多情况下提升性能
• 和前向的 normalization 相比，norm 操作之中因为均值和方差而引入的梯度在稳定训练中起到了更大的作用

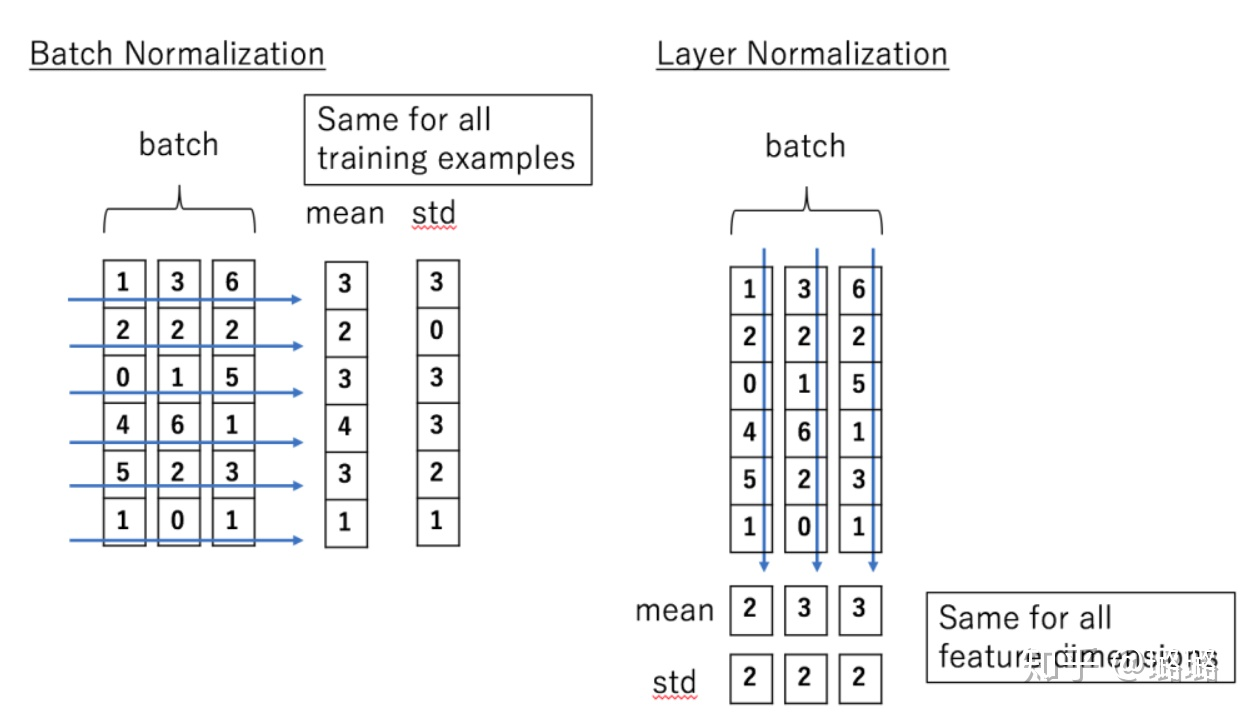
BN vs LN

BatchNorm是对一个batch-size样本内的每个特征[分别]做归一化，LayerNorm是[分别]对每个样本的所有特征做归一化。

理解

        [样本1的特征1,  样本1的特征2,  样本1的特征3]   <- 样本1
矩阵 =  [样本2的特征1,  样本2的特征2,  样本2的特征3]   <- 样本2
        [样本3的特征1,  样本3的特征2,  样本3的特征3]   <- 样本3
        \____特征1__/   \____特征2__/   \____特征3__/
                ↓               ↓               ↓

• BN (批归一化)：
  • 对 特征1列：计算 样本1的特征1, 样本2的特征1, 样本3的特征1 的均值和标准差，然后归一化这一列。
  • 对 特征2列：同样计算 样本1的特征2, 样本2的特征2, 样本3的特征2 的均值和标准差，归一化这一列。
  • 以此类推。
  • 箭头方向： 📍 沿着 列方向（↓），跨行（样本）操作。
• LN (层归一化)：
  • 对 样本1行：计算 样本1的特征1, 样本1的特征2, 样本1的特征3 的均值和标准差，然后归一化整行。
  • 对 样本2行：计算 样本2的特征1, 样本2的特征2, 样本2的特征3 的均值和标准差，归一化整行。
  • 以此类推。
  • 箭头方向： → 沿着 行方向（→），跨列（特征）操作。

适用场景不同

1. 依赖关系：

   • BN： 依赖于一个足够大的批次(Batch Size) 来计算稳定的均值和标准差。如果Batch Size太小（比如只有1或2），计算出来的均值和标准差波动会非常大，效果会很差甚至有害。
   • LN： 不依赖其他样本，也不需要大Batch Size。因为它只用自己的信息来归一化自己。在小批量甚至单个样本上也工作得很好。

2. 对序列数据的友好度：

   • BN： 处理固定长度的数据（如图像）很好，但在处理变长序列数据（如句子、语音）时就麻烦了。不同序列长度不同，统计量计算不一致，难以标准化。RNN/LSTM/Transformer等网络结构在训练时很难用BN。

   • LN： 天然适合序列模型和变长数据！因为它对每个样本（每个时间步）独立做归一化，不管其他样本（时间步）的数据。这就是为什么Transformer等模型普遍用LN而不是BN。

     我是中国人我爱中国

     武汉抗疫非常成功0

     大家好才是真的好0

     人工智能很火000

     上面的4条文本数据组成了一个batch的数据，那么BN的操作的时候

     就会把4条文本相同位置的字来做归一化处理，例如：我、武、大、人

     这里就破坏了一句话内在语义的联系。

     而LN则是针对每一句话做归一化处理。例如：我是中国人我爱中国——归一化处理后，一句话内每个字之间的联系并没有破坏。从这个角度看，LN就比较适合NLP任务，也就是bert和Transformer用的比较多。

3. 训练和预测的一致性：

   • BN： 训练时用当前批次的统计量，预测时用的是整个训练数据估算的（移动平均）固定统计量。训练和预测的行为略有差异。
   • LN： 不管是训练还是预测，它都只依赖于当前样本自身的统计量来计算归一化。训练和预测的行为是一致的。

特点	Batch Normalization (BN)	Layer Normalization (LN)
归一化方向	垂直方向（列方向） - 跨样本归一化同一特征	水平方向（行方向） - 在同一个样本内归一化所有特征
依赖样本关系？	是的，依赖一批样本中的其他样本	不，只依赖当前样本本身
对Batch Size的要求	要求较大的Batch Size (e.g., 32, 64)	不敏感，在小Batch Size甚至单样本下有效
适合数据类型	固定长度的数据 (如图像)	变长序列数据 (如文本、语音、RNN/Transformer)
训练/预测一致性	需要特殊处理 (用Running Mean/Variance)	天然一致
常见应用领域	Convolutional Neural Networks (CNN)	Transformers, RNNs, LSTMs, NLP任务

Reference

关于batch normalization和layer normalization的理解_bn和ln原理-CSDN博客

Layer Normalization - 半夜打老虎 - 博客园