梯度

梯度<–方向导数<–偏导数<–导数

导数对应一元(单变量)函数，表示一元函数在该点的变化率.
偏导数对应多元(多变量)函数，表示多元函数在该点沿坐标轴方向的变化率.
方向导数是偏导数概念的推广，表示多元函数在该点沿某一方向的变化率.
梯度是特殊的方向导数，表示多元函数在该点沿该方向变化率最大(该方向为梯度的方向，变化率为梯度的

导数

导数对应一元(单变量)函数，表示一元函数在该点的变化率.

一元函数在坐标系中表示为曲线，其几何意义为函数在该点切线的斜率，其本质是通过极限的概念对函

数进行局部的线性逼近.

例如：计算曲线 f(x) 上A、B两点的斜率K，B无限趋近于A，即表示为

K = \frac{f (x_{A} + Δ x) - f (x_{A})}{Δ x} (Δ x \to 0)

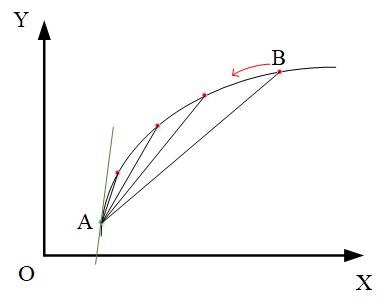
此时，K便表示曲线在A点处的斜率/变化率，亦称之为函数 f(x) 在该点处的导数

f^{^{'}} (x_{A}) = lim_{Δ x \to 0} \frac{f (x_{A} + Δ x) - f (x_{A})}{Δ x}

偏导数

偏导数对应多元(多变量)函数，表示多元函数在该点沿坐标轴方向的变化率.

图文描述时，一般以二元函数为例(更高元的函数也画不出来)，下图为二元函数 z = f ( x , y )

$\frac{\partial f}{\partial x} / f_{x} (x, y)$ 表示函数沿x轴方向的变化率(此时y视为常量)

$\frac{\partial f}{\partial y} / f_{y} (x, y)$ 表示函数沿y轴方向的变化率(此时x视为常量)

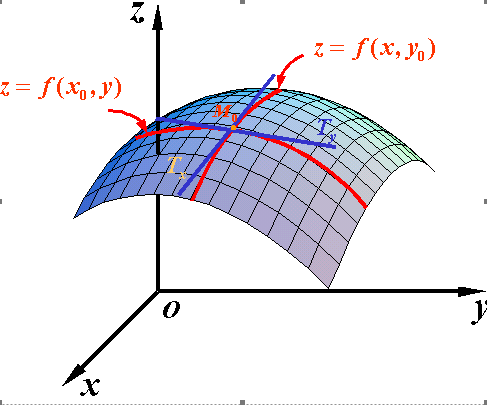
方向导数

方向导数是偏导数概念的推广，表示多元函数在该点沿某一方向的变化率

在可微分的情况下，方向导数可以被偏导数线性表示

假设求向量u方向上的方向导数，如下计算

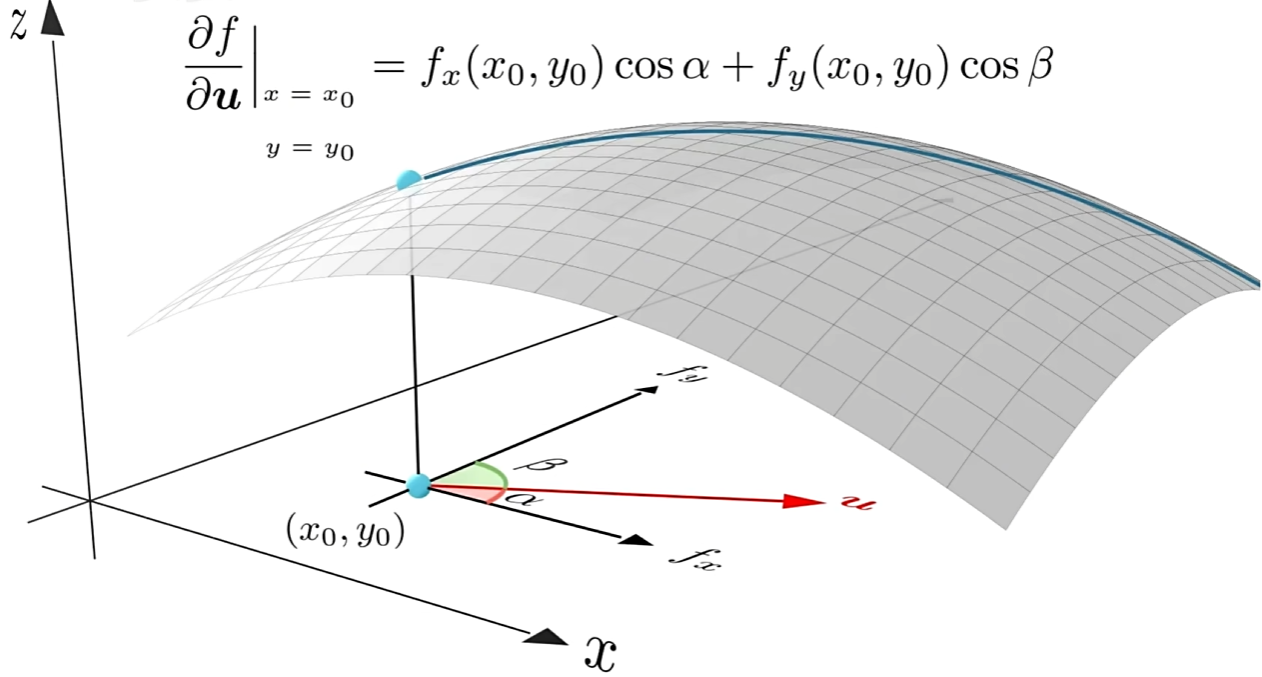
将方向导数的公式用向量点积的形式改写

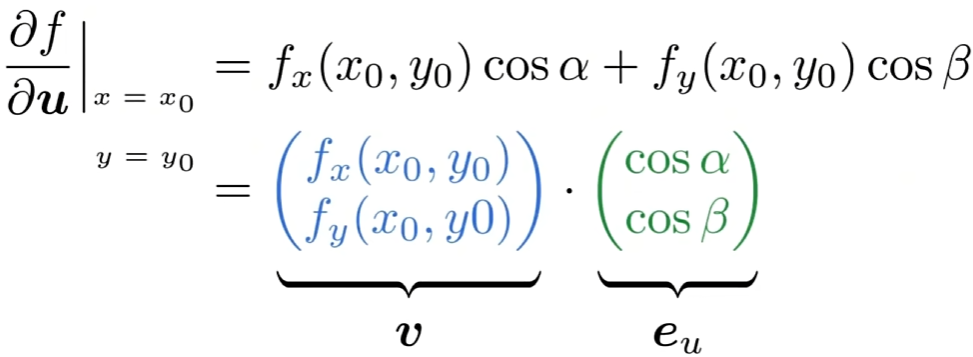
那么,这个式子就说明,方向导数是向量v在 $e_{u}$ 上的投影

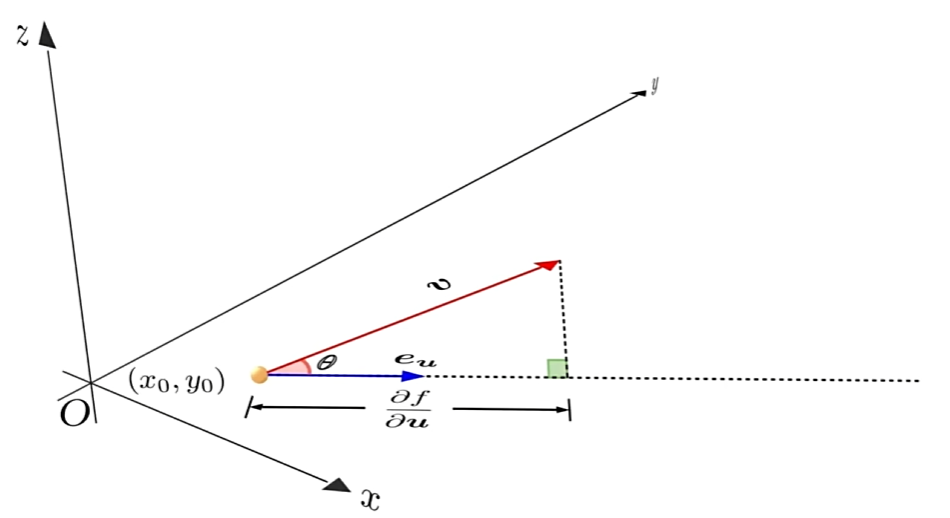
当theta不断靠近零时,向量v在 $e_{u}$ 方向上的投影也在不断的扩大

而当 $e_{u}$ 与V同向时，所得投影获得最大值，这说明,向量v的模长，即为方向导数中的最大者

向量v就是函数f在此点处的梯度

梯度

==梯度的值是方向导数中的最大值==

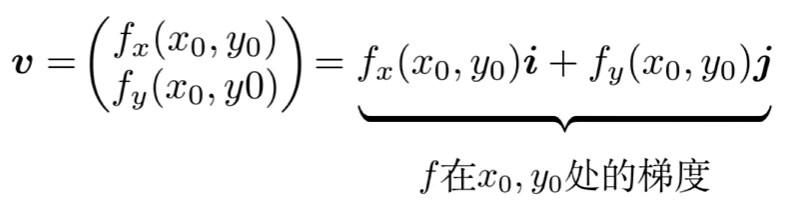
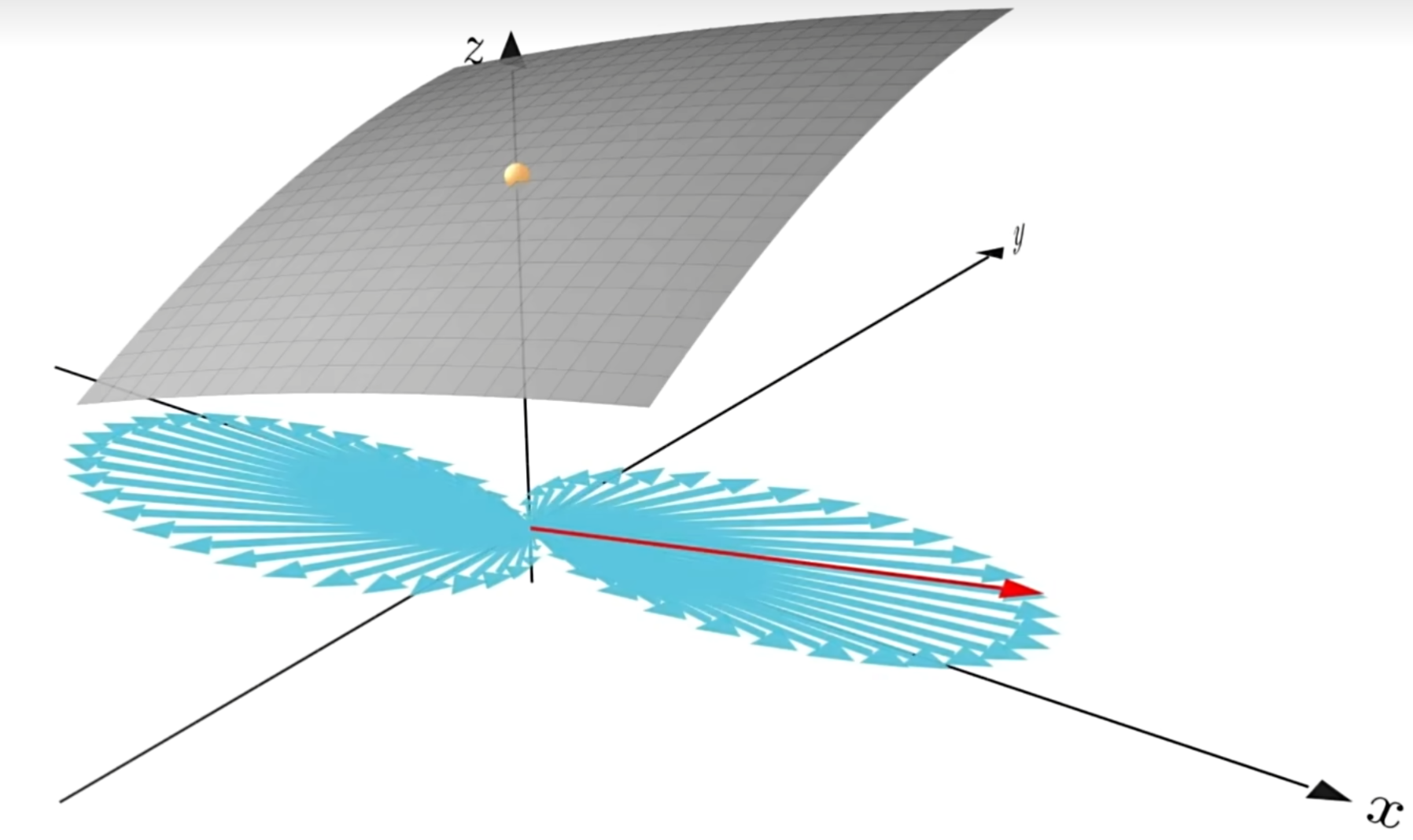
下图蓝色向量是某二元函数在（0，0）点处所有的方向导数，红色向量为梯度

方向导数

反之，函数在U方向上的方向导数，等于梯度在其方向上的投影

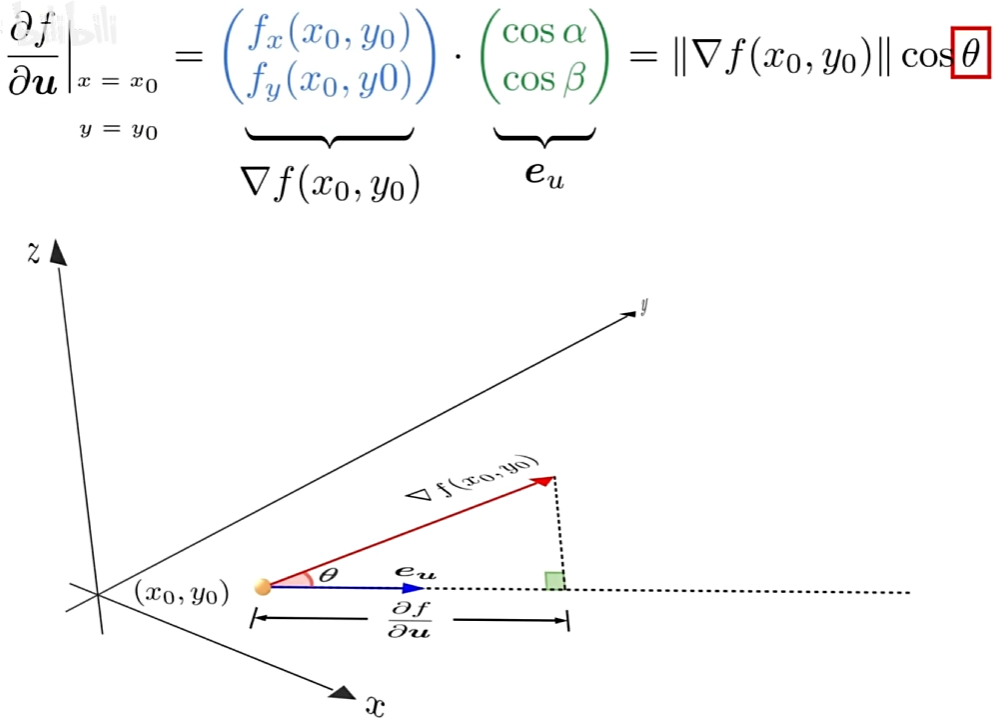
当θ= $\frac{1}{2} π$ 时，方向导数为0

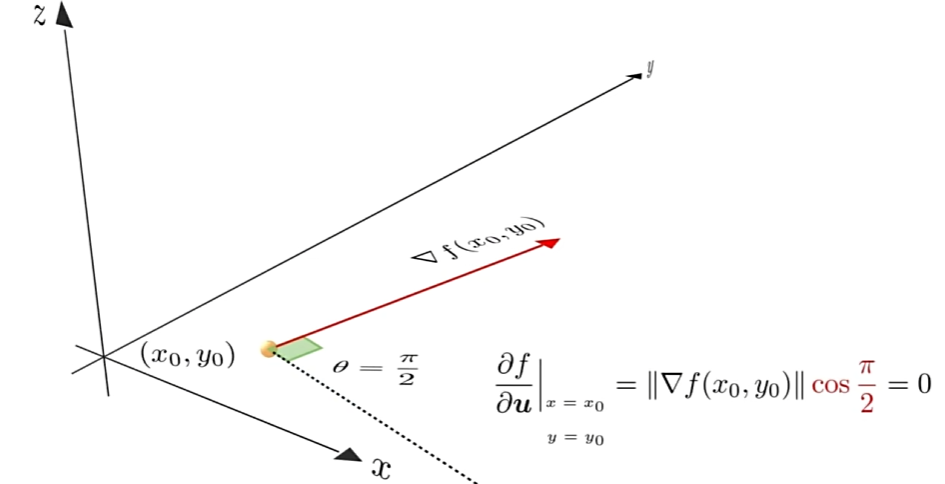
在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向这也就说明了为什么我们需要千方百计的求取梯度！我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的方向一直走，就能走到局部的最低点

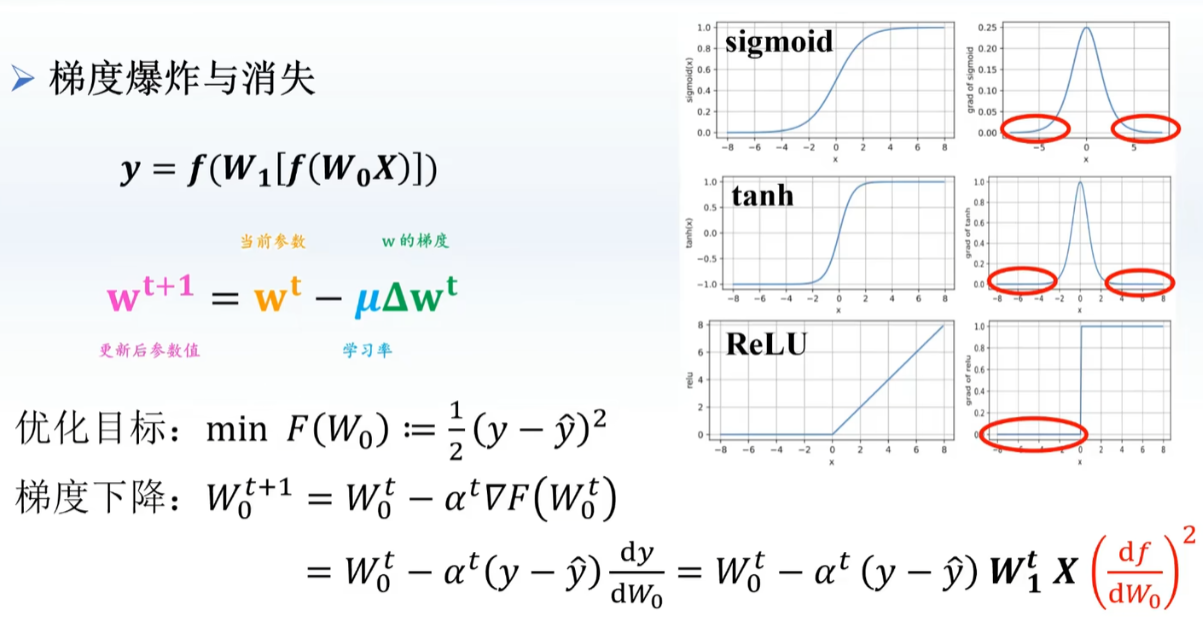
跳过几个激活函数系数就能降低多少

梯度 ​

导数 ​

偏导数 ​

方向导数 ​

梯度 ​

梯度

导数

偏导数

方向导数

梯度